Jacobi Exercise 3

Exercise 3: Jump on in, the water is fine ? MPI - 1D Decomposition

Objectives

  1. To think about distributed memory parallelization of an algorithm from the ground up.
  2. Get some experience with asynchronous communication MPI calls.

You can move on when you?

You have completed a 1-dimensional decomposition of the Jacobi Iterator algorithm that is data distributed and completed your scaling runs.

Description

Any parallel programmer worth their weight in salt needs to be proficient in MPI, which is the most basic of data-distributed programming models. Based on the lectures you have had during the workshop, you have been significantly exposed at to this model. While OpenMP is a quick and easy way to eek parallelism out of a serial program, MPI requires the programmer to think much more about data layout on each processor, due to the independent memory spaces. As you found out in Exercise 2, OpenMP can only take you so far, if you want to write algorithms that scale to 10,000?s processors, you must learn to exploit distributed memory model.

In this exercise, the programmer should spend some time on paper drawing out the algorithm, and thinking conceptually about the parallelism inherent in the program, otherwise, a lot of time will be spent spinning your wheels with minute details. Parallel programming is not about the language; it is about dividing the data and the work appropriately. Keep that in mind.

Here, we ask the programmer to come up with an algorithm that divides the work into 1 dimensional blocks, one of each residing on each processor in the computation. The output should be the same as the serial code (which is why it is always good to have a working serial version of the code available to test).

Instructions

The parameters of the algorithm are such:
  1. The grid matrix must be completely distributed, no replicating the matrix on all processors.
  2. The whole process must be parallel, that includes initialization of the grid and boundary conditions.
  3. Only asynchronous MPI_Isend and MPI_Irecv can be used for communication between processors.
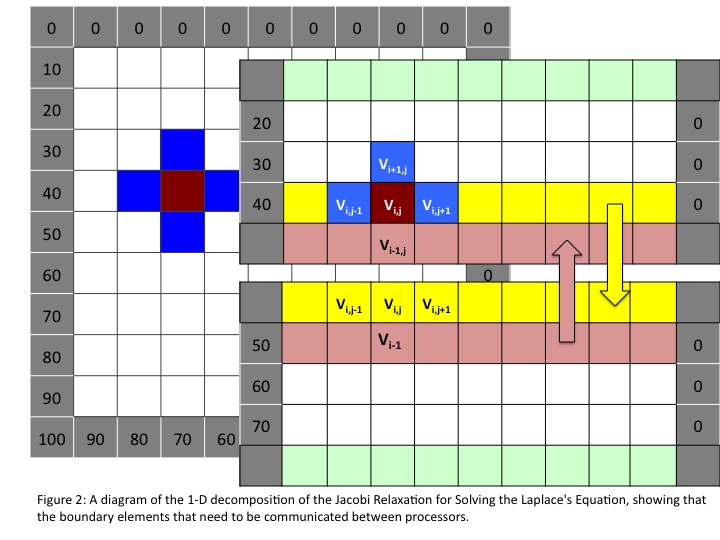
  4. In this exercise, only use a 1 dimensional decomposition (see Figure 2).
This is your first chance to design a parallel code from the start. Here is a guideline for the process that parallel programmers use to do this:
  1. Study the serial algorithm and see where parallelism can be exploited. Also think about how the data can be divided. Best way to do this is on a piece of paper, drawing out the layout conceptually before you even touch the code.
  2. Still on paper, figure out how this conceptualization moves to being expressed in the parallel programming language you want to use. What MPI calls do you need to use? Which processors will be doing what work? STILL ON PAPER.
  3. Now begin programming the algorithm up in MPI.
  4. Test the program on a small matrix and processor count to make sure it is doing what you expect it to do. Utilize the small debug queues on the HPC machine, or if you have MPI on your laptop or desktop develop there.
  5. Once you are satisfied it works, scale it up.
With this in mind, go through this process to implement a 1-D decomposition of the Jacobi iteration algorithm.

When you are satisfied you code is working, submit to the <batch queue> of your HPC architecture scaling runs for 100 iterations of the following sizes:
  • Matrix Dimension: 1024, 4096, 65536
  • Core Counts, 4, 16, 64, 256, 1024, 4096
Make a plot of the <parallel scaling> of these runs.

For Athena, you may need the following environment: 
MPICH_PTL_SEND_CREDITS -1

MPICH_MAX_SHORT_MSG_SIZE 8000

MPICH_PTL_UNEX_EVENTS 80000

MPICH_UNEX_BUFFER_SIZE 100M

Tips

  • To set up the initial matrix, you will need to figure out which values go in what chunk of the distributed matrix. This is not trivial. Many parallel programmers tend to forget that the initial setup if all part of the process, and in then end, can be a huge serial bottleneck in scaling up to 10000's core. No cutting corner! Think carefully about the data that each parallel chunk of work needs to have on it.
  • Notice the value of each matrix element depends on the adjacent elements from the previous matrix. In the distributed matrix, this has consequences for the boundary elements, in that if you straightforwardly divide the matrix up by rows, elements that are needed to compute a matrix element will reside on a different processor. Think carefully about how to allocate the piece of the matrix on the current processor, and what communication needs to be performed before computing the matrix elements. Figure 2 is an illustration of one communication patter that can be used.
  • You should be able to complete this exercise without the MPI_Barrier call.
  • It may also helpful to write a function that will print the distributed matrix, so that you have the ability to check to see if things are going the way you want.
  • Keeping the MPI_Requests straight is key. You will need MPI_Wait calls to make sure all asynchronous calls have been completed before proceeding onto the computation of the matrix elements, and if you call MPI_Wait on ranks that have not had any communication calls, the program will lock.
  • Use the function MPI_Wtime to time your code.
  • A reference of MPI routines can be found at: http://www.mcs.anl.gov/research/projects/mpi/www/www3/

Questions

  1. What are the inherent limitations of this algorithm? Are there constraints on the overall scalability and memory requirements?
  2. One question that a parallel programmer must continually ask themselves is what is the scaling of the communication my parallel algorithm has. Can you come up with an analytic expression for the number of values that need to be communicated at each iteration of the Jacobi iteration algorithm?
  3. Does the program scale? Are the results what you expected? If not, can you figure out why?

Extra Credit

  1. Can you add an OpenMP call to your solution and make it a hybrid algorithm? Does this scale better than the your straight MPI algorithm? (Hint: You can essentially put it in the same place as in the above exercise).

Hints

  1. A pseudo code version of this implementation can be found <link> here if you are having problems getting started.
  2. A full solution to the exercise is here for C/C++ and FORTRAN.