Molecular Dynamics Exercise 3
Exercise 3: Jump on in, the water is fine ? MPI Molecular Dynamics
Objectives
- To think about distributed memory parallelism of an algorithm from the ground up.
- Get some experience with asynchronous communication MPI calls.
You can move on when you?
You have completed a parallel decomposition of the Molecular Dynamics algorithm that is data distributed and completed your scaling runs.Description
Any parallel programmer worth their weight in salt needs to be proficient in MPI, which is the most basic of data-distributed programming models. Based on the lectures you have had during the workshop, you have been significantly exposed at to this model. While OpenMP is a quick and easy way to eek parallelism out of a serial program, MPI requires the programmer to think much more about data layout on each processor, due to the independent memory spaces. As you found out in Exercise 2, OpenMP can only take you so far, if you want to write algorithms that scale to 10,000?s processors, you must learn to exploit distributed memory model.In this exercise, the programmer should spend some time on paper drawing out the algorithm, and thinking conceptually about the parallelism inherent in the program, otherwise, a lot of time will be spent spinning your wheels with minute details. Parallel programming is not about the language; it is about dividing the data and the work appropriately. Keep that in mind.
Here, we ask the programmer to come up with an algorithm that divides the work amongst the processors, distributing numbers of cells to each cores. The trick comes in what data needs to be available to each cell in order to compute all of the forces inside. Obviously no communication needs to be done to compute the forces between atoms in a cell, but to compute the forces form atoms outside the cell, one will need all of coordinates from the atoms in adjacent cells. There is a large amount of overlap in computation that can be done while communicating, let?s see how much you can find.
Instructions
The parameters of the parallel algorithm are such:- All of the atoms in the system must be stored in distributed memory, and parallelism should be performed over cells.
- Everything must be parallel, including the creation of the initial set of atoms.
- Only asynchronous MPI_Isend and MPI_Irecv can be used for communication between processors.
- The program must print out the total energy for the whole system at each iteration.
This is your first chance to design a parallel code from the start. Here is a guideline for the processes that parallel programmers use to do this:
- Study the serial algorithm and see where parallelism can be exploited. Also think about how the data can be divided. Best way to do this is on a piece of paper, drawing out the layout conceptually before you even touch the code.
- Still on paper, figure out how this conceptualization moves to being expressed in the parallel programming language you want to use. What MPI calls do you need to use? Which processors will be doing what work? STILL ON PAPER.
- Now begin programming the algorithm up in MPI.
- Test the program on a small atom and processor count to make sure it is doing what you expect it to do. Utilize the small debug queues on the HPC machine, or if you have MPI on your laptop or desktop develop there.
- Once you are satisfied it works, scale it up!
- Number of Atoms: 1000, 10000, 100000
- Core Counts: 4, 16, 64, 256, 1024, 4098
Tips
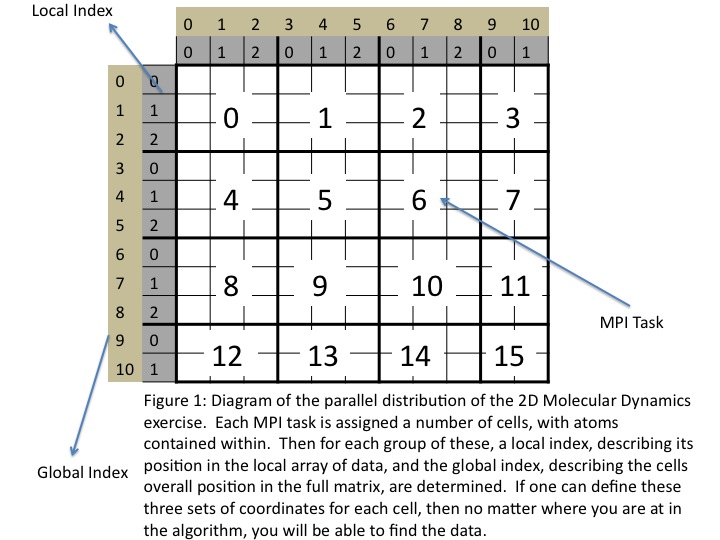
This algorithm can be very tricky to get working, there are a number of areas to get tripped up. Also, there is more than one way to do this. Below is a brief outline of a procedure that can lead to solution. It utilizes a replicated data map of the cell layout. While it is best to avoid using any replicated data, the size of this map should be relatively small so should not lead to any serious bottlenecks in our exercise.- First, you must figure out how to assign the cells to processors. In this example, you should divide them up evenly amongst the cores. Figure 1 shows the layout chosen for the solution problem set.
- There are some fundamental values that need to be defined:
- The number of cores must be a perfect square, so you can have an integer dimensions.
- You must figure out how to define the dimensions of the local data too.
- These are tricky write them down and graph it out. If you cannot get it after a while, look at the beginning of the solution, it shows how.
- Once you know this, create a map that is the same dimensions as the full matrix. In each element of this matrix, you want to store the number of atoms and the processor to which each cell is assigned. This is similar to the CellSizes matrix in the serial example, with added information. It is acceptable to compute the map on one core and broadcast it to the others.
- Now that the data layout is know, you can run through and populate all of the cells with atoms, this is pretty straightforward and very similar to the serial version.
- Now we can begin timesteps. In order for each cell to be able to compute all of the forces for the atoms inside, it will need all of the coordinates from all of the adjacent cells to be communicated to it at the beginning of each timestep. This should be done asynchronously. In this example, edge cells do not pass their coordinates beyond the boundaries, so that must be taken into account.
- Communications Tidbit #1: The way to accomplish the communication is loop through each cell, post the Irecv's and Isends, and then post an appropriate MPI_Waitall with the right number of variables. Keep in mind, all fo the inner cells will have 8 messages being sent from and recieved to, save for the edge cells. If you don't post the right amount of MPI_Waitalls, the code will lock.
- Communications Tidbit #2: It is easiest if you treat all intercell transfers as communication, even if they are on the same processor. Including logic to exclude communication between cells on the same processor is not necessary and should not hinder performance.
- Communications Tidbit #3: You will need to have space allocated for each cell to recieve the coordinates of the cells communicating with it. Since it is not garunteed that each cell will hold the same amount of atoms, you will need to communicate the number of atoms as well. You could pack this in the messages sent out.
- Communications Tidbit #4: Tags are your friend. You will be sending a lot of messages, many to the same processors. Using tags will be absolutly essential to makeing sure that messages get to where they need to go.
- Communications Tidbit #5: The communications is where having the ability to map the cells to processors comes in very handy. Utilize the map created above to tell which processors each communications needs to be sent.
- NOTE: You can compute the forces of atoms with other atoms inside their own cell while communicating. This is a good chance to learn why asyncronous communication rocks!
- Once the messages arrive, you can compute the rest of the forces, integrate, and move on.
- Think very carefully about how to do this one before proceeding to program it up, if you are not prepared going in, you will get lost quickly.
- Utilize the serial code to make sure you are getting things right in the parallel code. It is always nice to have a nice serial code around for this purpose.
- Use the function MPI_Wtime to time your code.
- A reference of MPI routines can be found at: http://www.mcs.anl.gov/research/projects/mpi/www/www3/
MPICH_PTL_SEND_CREDITS -1
MPICH_MAX_SHORT_MSG_SIZE 8000
MPICH_PTL_UNEX_EVENTS 80000
MPICH_UNEX_BUFFER_SIZE 100M
Questions
- One question that a parallel programmer must continually ask themselves is what is the scaling of the communication my parallel algorithm has. Can you come up with an analytic expression for the number of values that need to be communicated at each iteration of the Jacobi iteration algorithm?
- Does the program scale? Are the results what you expected? If not, can you figure out why?
- Are there other items in your code that could be parallelized further to improve scalability?
Extra Credit
- Can you add an OpenMP call to this and make it a hybrid algorithm? Does this scale better than the your straight MPI algorithm?
- There is a "bug" in this code that makes it easier to write. If a particle moves out of one cell into another cell, it is still tracked as being in the original cell. Can you figure out how to alleviate this "bug".
Hints